코딩초보 김씨
[R] 다중 변수 자료의 분석 본문
1. 산점도 (scatter plot)
1) 두 변수 사이의 산점도
(예시 : mtcars 데이터)
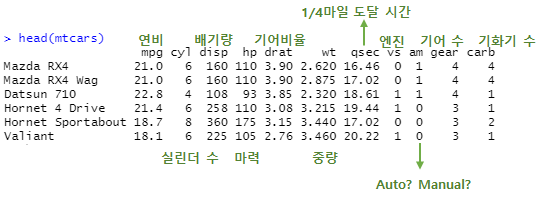
wt <- mtcars$wt # 중량 자료
mpg <- mtcars$mpg # 연비 자료
plot(wt, mpg, # x축, y축 자료
main="중량-연비 그래프",
xlab="중량",
ylab="연비(MPG)",
col="red",
pch=19) # point의 종류
2) 여러 변수들 간의 산점도
(예시 : mtcars 데이터)
vars <- c("mpg",'disp','drat','wt') # 변수 지정
target <- mtcars[,vars]
head(target)
pairs(target,
main="Multi Plots")
3) 그룹 정보(Label)가 있는 두 변수의 산점도
(예시 : iris 데이터)
iris.2 <- iris[,3:4] # 데이터 불러오기 (iris Petal Length & Petal Width)
point <- as.numeric(iris$Species) # Label 값 불러오기
color <- c("red","green","blue")
plot(iris.2, # 데이터 입력
main="iris plot", # 제목
pch=c(point), # 점의 모양 : 0~25, 문자(O,a,@,#등)
col=color[point])
2. 상관분석 (correlation analysis)
: 얼마나 선형성을 보이는지 수치상으로 나타낼 수 있는 방법
• 피어슨 상관계수 (-1 ≤ r ≤ 1)
1) r > 0 : 양의 상관관계
2) r < 0 : 음의 상관관계
3) r이 1이나 –1에 가까울수록 x, y의 상관성이 높고, 0에 가까우면 상관성이 낮다
1) 상관 계수 계산 (correlation coefficient)
(예시 : iris 데이터)
cor(iris[,1:4]) 2) 상관 분석 (correlation analysis)
(예시 : 음주 정도beer와 혈중알콜농도bal의 상관성 조사)

# 데이터 생성
beers <- c(5,2,9,8,3,7,3,5,3,5)
bal <- c(0.1,0.03,0.19,0.12,0.04,0.0095,0.07,0.06,0.02,0.05)
tbl <- data.frame(beers,bal)
# scatter plot
plot(bal~beers, data=tbl)
# 회귀식 도출
res <- lm(bal~beers,data=tbl)
# 회귀선 그리기
abline(res)
# 상관계수 계산
cor(beers,bal)
> cor(beers,bal)
[1] 0.6797025
3. 꺾은선 그래프
: 시계열 자료(times series data, 시간의 변화에 따라 수집한 자료)의 내용을 파악하는 가장 기본적인 방법
1) 단일 선그래프
(예시 : 한 학급의 월별 지각생 통계를 선그래프로 표현)

# 데이터 생성
month <- 1:12
late <- c(5,8,7,9,4,6,12,13,8,6,6,4)
# 그래프 그리기
plot(month,
late,
main='지각생 통계',
type='b', # l:line만, b/o:원형점, s:계단모양
lty=1, # line type
lwd=1, # line width
xlab='month',
ylab='late cnt'
)
2) 복수 선그래프
month <- 1:12
late1=c(5,8,7,9,4,6,12,13,8,6,6,4)
# 데이터 추가
late2=c(4,6,5,8,7,8,10,11,6,5,7,3)
plot(month, late1,
main='지각생 통계',
type='b', # l : line만, b,o:원형점, s : 계단모양
lty=1, # 1~6까지
col='red',
lwd=1,
xlab='month',
ylab='late cnt'
)
# 그래프에 line 추가
lines(month, late2,
type='b',
col='blue')
★★ 4. 데이터 세트 정보 분석 ★★
(예시 : Bostin Housing 데이터 중 5개 변수)

1. 분석 대상 데이터 준비
(라이브러리 설치 : Rstudio → Window4:파일창 → Packages → Install → "mlbench" → install)
library(mlbench)
data("BostonHousing")
# 변수 5개 추출하여 mydata 객체에 저장
mydata <- BostonHousing[,c("crim","rm","dis","tax","medv")]
2. 데이터 전처리 : grp 변수 추가 (grp : 주택 가격을 상(H), 중(M), 하(L)로 분류한 것)
# 빈 grp 객체 생성
grp <- c()
# mydata의 medv주택가격 column 값을 기준으로 grp 값 지정
for (i in 1:nrow(mydata)){
if (mydata$medv[i]>=25.0){
grp[i] <- "H"
} else if (mydata$medv[i]<=17.0){
grp[i] <- "L"
} else {
grp[i] <- "M"
}
}
# vector를 factor로 변경, level 순서 지정
grp <- factor(grp)
# mydata에 grp column 추가
mydata <- data.frame(mydata, grp)
3. 데이터셋의 형태와 기본적인 내용 파악
str(mydata)
head(mydata)
table(mydata$grp) # grp별 분포4. 히스토그램에 의한 관측값의 분포 확인
(예 : rm, medv는 정규분포 모양으로 데이터 분포)
par(mfrow=c(2,3)) # 2*3 화면 가상 분할
for (i in 1:5){
hist(mydata[,i], main=colnames(myds)[i], col='yellow')
}
par(mfrow=c(1,1)) # 가상 분할 해제
5. 상자그림에 의한 관측값의 분포 확인
(예 : crim(1인당 범죄율)은 값의 편차가 작게 분포하고, tax(재산세율)은 값의 편차가 크다)
par(mfrow=c(2,3))
for (i in 1:5){
boxplot(myds[,i], main=colnames(myds)[i])
}
par(mfrow=c(1,1))
6. 그룹별 관측값 분포의 확인
(예 : 주택 가격이 낮은(L) 지역의 범죄율이 높고, 주택 가격이 높으면(H) 방의 개수가 많다)
boxplot(myds$crim~myds$grp, main='1인당 범죄율')
boxplot(myds$rm~myds$grp, main='방의 개수')
7. 그룹 정보를 포함한 다중 산점도(scatter plot)를 통한 변수 간 상관 관계의 확인(correlation analysis)
point <- as.integer(myds$grp)
color <- c("red","green","blue")
pairs(myds[,-6],pch=point, col=color[point])
8. 변수 간 상관계수(correlation coefficient)의 확인
• 피어슨 상관계수 (-1 ≤ r ≤ 1)
1) r > 0 : 양의 상관관계
2) r < 0 : 음의 상관관계
3) r이 1이나 –1에 가까울수록 x, y의 상관성이 높고, 0에 가까우면 상관성이 낮다
cor(myds[,-6])
'R' 카테고리의 다른 글
| [R] 다중변수 자료의 분석 - 복습 문제 & 정답 (0) | 2021.06.21 |
|---|---|
| [R] 단일변수 자료의 분석 - 복습 문제 & 정답 (0) | 2021.06.21 |
| [R] 조건문, 반복문, 함수 - 복습 문제 & 정답 (0) | 2021.06.19 |
| [R] 행렬과 데이터프레임 - 복습 문제 & 정답 (0) | 2021.06.19 |
| [R] 단일변수 자료의 분석,탐색 방법 (0) | 2021.06.18 |


